Scaffolding Trig Graphs - Desmos Kong

Yesterday evening, way too late to be planning a new lesson I was noodling through Sam Shah's filing cabinet looking for something that would allow students to practice trig functions, ideally kind of game like. There is good stuff there, like this graphic organizer from Mimi, but nothing like what I was looking for. For years, here and there, I have heard people mention the graphing game Green Gobs but I have never actually used it myself. Still, downloading software for all of my students to use (that had to be purchased) was going to be out of the question, at least last night. Maybe I could make something similar with Desmos. I have been using Desmos more and more with the kids and loving it. A little while later I came up with Trig Scaffolding.

Anyway, let's get into it. The activity (1) I created is called Trig Scafolding: How High Can You Get? The entire thing is built into one Desmos worksheet. I demoed the activity for my students on the big screen and then shared the link.

I think this is all best explained with screen shots:

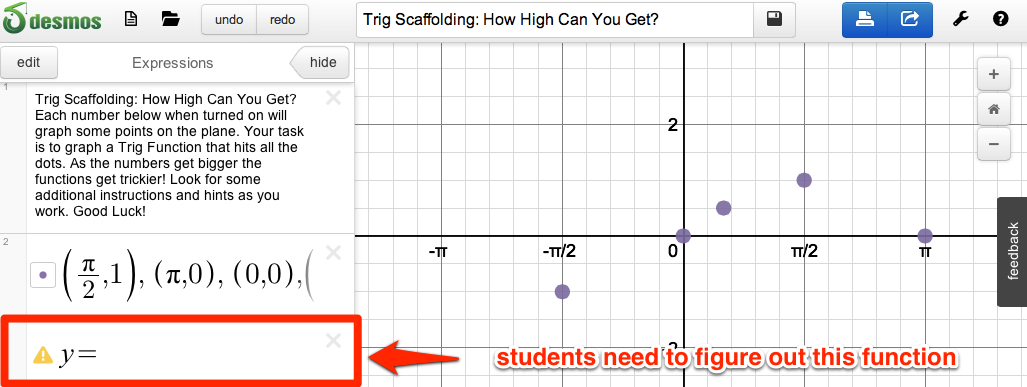
When students open up the Desmos Link they see the points of the function they are trying to graph.

Students know they are right if their graph matches up with the points.

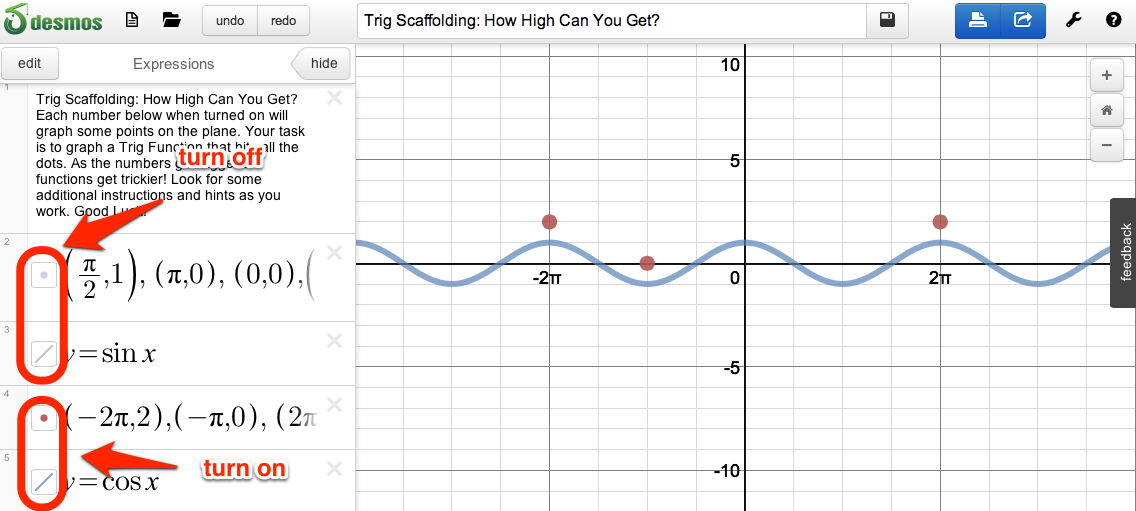
The kids can «climb up» to the next graph by turning off the graphs they were working on and turning on the next ones.

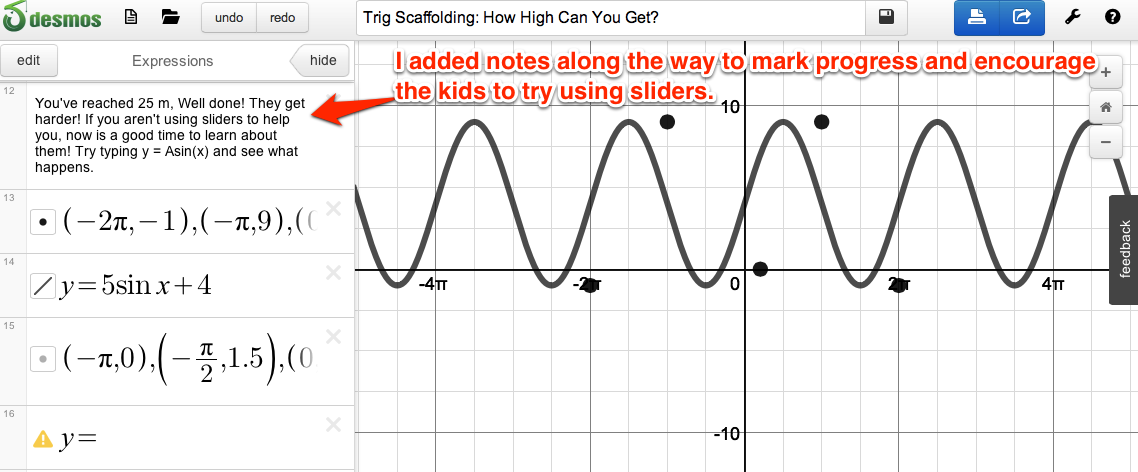
I added notes along the way in Desmos to mark students progress and remind them about Desmos's excellent features like the easy integration of sliders. I spent the entire activity circulating and working with pairs of students. I was impressed with the total engagement the kids had through the block and the different strategies they were using to figure out the graphs.

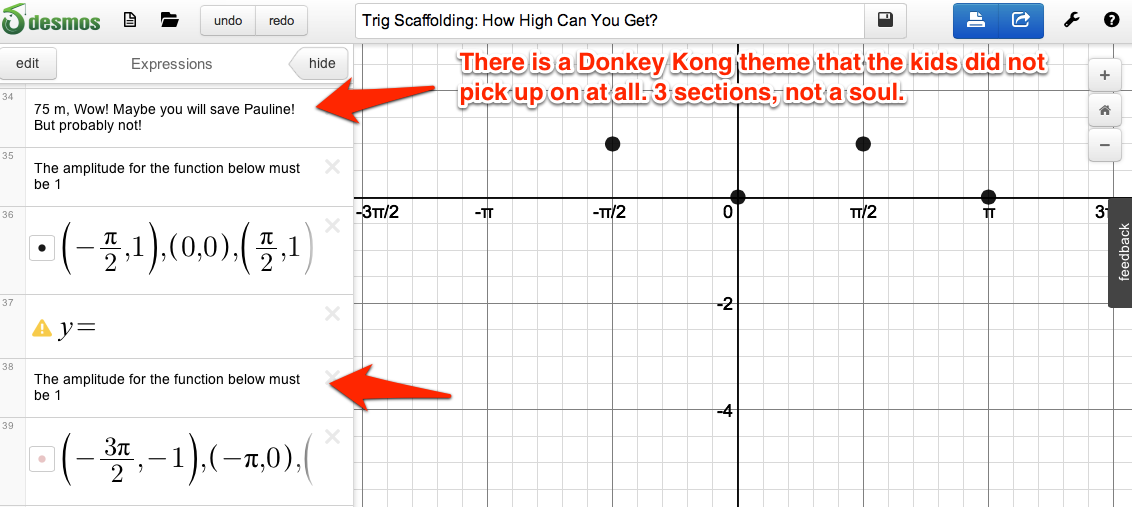
No one picked up on the very thin Donkey Kong theme, but overall the activity worked really well. A couple groups did engage in some mindless guessing and checking, but most of the kids were really trying to reason out the functions with Desmos along with pencil and paper or whiteboards. Although I didn't do so, it would be easy for students to turn in their «solutions» for this assignment by having them save their graph and sharing the link with you.

I was really unsure how difficult kids were going to find this when I created it, but the scaffolding of the problems seemed to be decent. It is easy enough to adjust anyhow. I think in the next iteration I will add more problems where I place restrictions on the graph, either to make the problems more challenging, or increase the level of scaffolding.

Have you tried anything like this with Desmos? I would love to see it and hear about it!

---

(1) I called it a game with my first class yesterday and the kids kept comparing it to other games like Danger Cards, I called it an activity in the other classes and there was none of this nonsense. In fact in the other classes the kids told me that it was «a good game!»

Passion, Trigonometry, & Locked Doors

The other day Rory posted a new problem solving method with a 75 letter acronym. I have no idea what it was, but the first letter was this.

P: What problem in my local community ignites my passion to the point of ​action?

On Friday at school I had a long conversation with John, a programmer who is working with ASB to design some gamification stuff. Looking around my classroom he saw the unit circles everywhere and exclaimed his love for trigonometry. «I need you to come talk to my students!» I exclaimed after he went on and on about how he uses trig all the time in the programs he writes. I wonder if he learned most of that trig when he really needed it for the coding, or it was all from tenth grade (I suspect the former).

Just like today when I finally learned how to break open a locked door with a credit card. I was standing in the doorway above, admiring my newly installed chin up bar, thinking «maybe tomorrow I will be able to do one chin up» when I closed the door to discover two things: first, the door could still close with the chin up bar in place (this should have been obvious) and, second, the door was now locked!

With no key, and a lock that was real (not one of those US bathroom locks that comes with a pin) it was time to hit the net. I had, of course, heard of using a credit card to open a locked door, but always figured it wasn't really possible with a real door or with a real lock. Luckily my computer was not in the locked room, so off to YouTube I went. Gold immediately, with a young man (maybe 12) clearly demonstrating how to open his front door with a credit card. I watched it a few times until I was convinced that I too could get into my locked bedroom, and I did. Here is the clip. John's desire to learn trigonometry was ignited by his passion for video games. I needed to learn lock picking to get into my bedroom. When passion is ignited learning follows.

Lesson Playback: A Trig Foldable

If I am not at the top of my game, my third algebra 2 class can be a challenge. I am usually able to finagle the schedule though so that my third class lands the day after I had a chance to teach a lesson in the first two sections and can hence make adjustments to it with them in mind. This can result in a class that can eclipse the quality of the first two.

Today I wanted to further consolidate our learning about the unit circle. There aren't really many blog entries here so it should be easy to catch up if you are interested. Last class we worked on the trig puzzle I created, most groups managed to solve it and many even worked out the quote. You know an activity is engaging when you get e-mails late at night proclaiming a solution or kids running into class doing the same. The six identities were more of a challenge. They would be today's focus.​

Usually it's 5 Minutes of ❤​.

Today instead of the normal routine we started class with a 3-minute brainstorm.​ ​I always time this stuff on my phone and the alarm is almost always the same song. Currently Eric Hutchinson's lovely Rock and Roll. When the alarm sounds the kids stop working and immediately begin singing along. Always, and no I did not tell them to do this, these traditions just begin. When I turn off the timer it is quiet again. After the three minutes were up I did a quick snowball activity. Basically all this means is the students crumple their paper up like a snowball (kind of foreign in Mumbai) and throw it somewhere else in the room. This is not my favorite activity but kids like throwing their paper at one another, and used sparingly (like once or twice a year) it works. Once everyone retrieved a new paper I set the timer to two minutes and had them add facts to the new sheet they had. ​After this round they passed their paper to a neighbor and added facts for one more minute.

Next I picked one of the front whiteboards (my classroom is a whiteboard paradise) and we did some rounds. I went around the room, student to student, and had each of them contribute a fact they thought were important to the whiteboard map. I scribed. In retrospect I probably could have had a student do this, although they were all busy adding facts they had still missed to their sheets. About halfway through this process I deadpanned that this was even more fun than Scattergories. Although it actually was fun, and everybody was engaged. With no classes up to this point resembling a traditional lecture, my kids had collectively figured out a lot about the unit circle.

Results of our group brainstorm.

​With a board full of information I told my students to indicate on their papers the three most important points we had put on the board and look up when they were done. Next I got them out of their seats and had them indicate their selections using asterisks or checks on the board.

​With a quick review of the unit circle over, it was time for arts and crafts. I had decided yesterday that I would try one of these «foldables» I endlessly see on math blogs, so we gathered round and Katie taught us how to make one of those fortune telling things.

Back to the front I went. I surmised from the previous day's lesson that while few of the students had figured out all six (three pairs) of the trig identities I had included in the puzzle, we could probably come up with them in a group brainstorm. It went really fast actually. Our fortune teller foldable would house this information.

Quick sketch of what the final draft ​should look like.

I split the kids into small groups for the next part of the activity that was a jigsaw. Each group had to sketch a diagram (with words if necessary) that would illustrate why their trig identity pairs were true. I gave them 9 minutes to come up with their diagrams and then each group presented to the others.​ During this time I moved from group to group to give advice and ask questions.

I had thought their might be a few minutes at the end of the block for students to fill in their foldables, but the block was about done. Students snapped photos of the whiteboards and will complete the task for homework.​

Draft explanation of two of the identities.​

So not the most exciting lesson ever, nor the review game I thought I was going to write about today, but a good example of a lesson on a day in ordinary time.​

Trig Puzzle

Generally reinventing the wheel is not the way to go with a math activity but I am a glutton for punishment sometimes. Years ago teaching pre-algebra I had made students a handwritten puzzle worksheet in which to solve they had to cut out the pieces and reassemble them into a box making sure to align the sides using exponent rules. This, I think, might have been inspired by a similar Pizzazz worksheet.

These ladies were on fire during this activity. Just outside my classroom are these awesome booths where students can work, love em.​

Anyhow, in one of my recent field trips through Sam's filing cabinet I remembered downloading something similar called a Tarsia puzzle. I would create one for my trigonometry students I figured. They had mastered the Unit Circle and I wanted to have them use the unit circle to have them think about some of the basic identities (odd, even, co-function etc.) I figured one of these puzzle worksheets could serve this purpose well. It might also be a nice bridge between the trig we had done so far and the next lesson I had originally planned about identities that I feared would be too hard. It turns out there is a free program to create these Tarsia puzzles (great resource here), but alas it is Windows only and at home I only have a Mac. Nevertheless the idea was gnawing at me so I decided to go for it and make my own.

I found the PDF I had downloaded from Sam's site (I can't seem to find the exact link) and opened it in Illustrator. From here I was able to delete all the original equations and add new ones I created in Math Type. Before I entered any equations into Illustrator I made a list of the six identities I wanted to focus on and made eighteen pairs that students would have to match. Next I drew the final shape for my puzzles' picture on paper and entered the equations to create the key. From here it was relatively easy to create the student version of the worksheet because I just cut up my key and entered my triangles into Illustrator. It was initially challenging to get the text rotated and oriented properly but by the time I had entered a few triangles of data I was a pro.  ​Additionally, I decided to add a couple layers to what was already a puzzle. First, I did not tell my students what final shape the triangles would be assembled into, and second I added a quote (that connects to the shape) that would reveal itself when the puzzle was completed. Further the quote has blanks that need to be filled in, making it even more challenging. I also figured that the blanks in the quote would make it more difficult for students to work the puzzle backwards. The quote also made it really easy to check to see if the puzzle was properly solved.

I've used this activity with two of my three algebra two classes so far and it has gone great. It is a little bit more difficult than I intended but in one class one group was able to crack the whole thing during the time allotted but just barely. Another group stayed behind after class to finish it. ​During the lesson I moved from group to group and helped students make connections between the puzzle and the unit circle, great lesson for a Friday afternoon math class.

Click through for a PDF version of the puzzle, editable in Illustrator if you have it.​

Trig Speed

After my students measured the Unit Circle using the worksheet I adapted from Riley. We spent a class period or so figuring out all of the «nice» coordinates around the circle. A few kids vaguely (to my dismay but not surprise) remembered special right triangles, and so I made sure that we (mostly students at the board doing the heavy lifting) derived these from scratch. Once we filled in the coordinates all the way around the circle. I also introduced them to angle measure in radians and had the kids work in small groups to find all of these. This was fun because different groups were developing different strategies to figure out the angles and the room was buzzing with the discovery of new new strategies and approaches. Once we figured out all the angles we went through the entire diagram again from scratch and I asked the students to spend a few minutes seeing if they could figure out strategies to reproduce our unit circle quickly since next class we would have a quiz.

The picture links to the PDF file.

The first unit circle quiz day is always a good time because students come in and I ask them if there is a new pop song they want to hear and they inevitably choose something obnoxious and this works out perfectly. This year one of the girls chimed in and said «Just play anything by Taylor Swift!» I could not ask for more. «I Knew Your Were Trouble» it was. ​The quiz works simply, students keep the worksheet facedown until the song begins and need to finish it before the song ends. It turns out «I Knew Your Were Trouble» is 3:40 seconds. More than enough time for the unit circle. Maybe even two.  

Maybe you are thinking «Why do I torture the kids this way!» Haha. Well I am not out to torture them. I tell them straight up I am preparing them to be trig experts in the IB (that they will pursue next year) and that being able to quickly produce this unit circle will get them great results. Every year students come back from previous years to tell me how much it helped. And the students find it fun. I do give the students a grade for the assignment, but not until the third time through (unless they think they finished it) and their low grades can be straight up replaced as students can finish the task. After each daily quiz I have students partner up with a peer to figure out errors and strategize, and then if necessary we work together as a class to clear up any class wide concerns. I encourage everyone to try to improve their score. If you are now thinking «Well why would you memorize anything?!» Then I suggest this great article from Wired back in 2008. ​

I still, of course, haven't brought up the idea of cosine and sine, but students are more and more mentioning SOHCAHTOA and I am more and more insisting they must mean CAHSOHTOA.

Gator Golf

I love review games. Occasionally in high school I got to plan review games for my classes and it was awesome (I know, I know I am wicked lame) Anyhow, I think I first heard of using Gator Golf for a review game from the book Rookie Teaching for Dummies but I can never leave well enough alone so here is my twist on it.

Setup:

Divide the kids up into four teams -do this any way you see fit. Give each team a portable whiteboard to write down their final answers, along with scrap paper and golf pencils (obviously) to make notes if necessary. You will also need to get the Hasbro game Gator Golf. I also went to Home Depot and got some putting green carpet, and some tees and a putting glove at a golf store, you could probably make due without these but I love little details. Dividing class into groups and giving each group a whiteboard is a strategy I use again and again for many review games and it works pretty well.

The Game

The game is played in multiple rounds

Round 1:

This round relies most heavily on the keynote presentation (see link below). In round 1 there are 16 multiple choice questions (the questions I included are all about trigonometry). When a question is revealed each team answers it on their whiteboard and then "locks in" the answer by flipping their board upside down. Once three of the four teams are locked in I cajole the last team into finishing as well. At this point the answers are revealed. The team in «control» reveals their answer first followed by the rest of the teams. If the team in control answers correctly they score a tee, if not, the next clockwise team has a chance to steal, etc. After each question is finished control passes to the next clockwise team around the room, the team in control is indicated by the location of the alligator in the slide deck.

Golf Round:

After the 16 questions are up I tally the tees that each team earned to determine each team's golf position. Sort of like in Hole In One on The Price Is Right (another post for another day) The team with the highest score gets to putt closest to the gator (but not too close). I usually wait until after the scores have been tallied to reveal the gator which always goes over very well. Prior to this just the green is on the floor and so the kids' curiosity is piqued. Everyone gets one putt, they score one point for hitting the gator at all, and three if the gator devours and spits out their ball. It is really important to allow the kids to have some fun golfing while also not getting so bogged down in the golfing part that no additional math gets done. If you move swiftly you should be able to get through the golfing business in no more than 7 minutes or so. If your class is enormous, you might want to have only half of each team golf during round one.

Yash lines up for a put.

Round 2:

Each team gets a few minutes to peruse the longer form questions from the round two document (included in the zip file) then I have the teams in reverse order of score select a question (or two based on time) that they want control of. After this selection each team gets a few minutes to work together on their questions and write up solutions on the classrooms whiteboards (not the mini ones) for everyone else to see. If teams have extra time they can try to solve the questions their team did not select in hopes of stealing another teams questions. Once time is up I score each question, one putt per correct answer and we golf once more. This golfing round goes much more quickly since there are a maximum of 10 puts, probably much less.

Final Round:

If there is time, I will have teams wager part of their score on one final putt. To determine the grand champion.

I actually didn't give any of the teams any prizes for winning the golf game this year, just the glory of being champions. Candy would work fine but is not really necessary, I would certainly advise against giving any sort of bonus points as a prize.

Other Thoughts:

I hadn't played this game in a few years, since the first gator met his demise, but I saw a new release of Gator Golf recently and picked up a copy. The game takes a bit of work to set up but always goes over very very well. I love tweaking rules and things so am always changing the games around to try to make them better. This time for example I had red tees and white tees mixed in my golf hat and when teams scored a point during round 1 they drew their tee out of the hat, red tees counted double. 

Whatever you do with the rules be sure to tell the kids what they are ahead of time and stick to them, kids go crazy when you change the rules in the middle of a game. Also during round one don't hesitate to stop the game and "go over" the tricky problems. This is a review game after all.

I wish I could stage shots like this.

Files: This file includes the Keynote slideshow I used for round one. Lately when I am making a slideshow for a game I create a Pages document with all the questions to begin with so I have included that document as well. I also included a copy of the Round 2 questions. These are both in PDF form also. The questions for this game are all about Trigonometry covering through trig equations but the game can easily be adapted for most other topics. 

*If I link to something for sale on Amazon it will most likely be an Amazon Affiliate link. Maybe someday these will pay for the blog (but as of this writing I have a click through rate of 0, which is not surprising because this blog is brand new, but anyway)

Measuring The Unit Circle & CAHSOHTOA

We started trig last week in Algebra 2. I began this time around with a trip online to see if I could find anything new to begin the unit with. I found this great post by Riley (via Sam Shah) about having kids measure the Unit Circle. A kind of sandbox approach. Anyhow it worked fantastically. In all three of my classes we were able to have great discussions about all the stuff that was learned by measuring this all out by hand. And I don't think anyone even asked «But Roy, when are we ever gonna use this?» In one of my classes the students got into a little debate reminiscent of Name That Tune's bid a note as they tried to lower the number of measurements that were actually needed to label all the points on the circle. I was sure they would figure out the various quadrants, but when they made the connections to the complementary angles within the quadrants I knew for sure this was the perfect activity to begin trig with.

First half of the first half of the worksheet.

Incidentally I took Riley's picture and turned it into a worksheet. Here is the file. I began class by having my students type their data into a Google Spreadsheet that I set up with them to calculate the mean of their scores. I plan on going back to this spreadsheet in the next couple of days and adding a cosine and sine value to it.

A couple of students know we are studying trig and have asked «Roy, does this have anything to do with SOHCAHTOA?» and I have been like «What is that? It sounds similar to CAHSOHTOA! Is that what you meant?»

First half of the second half of the worksheet.